|
|
Internet-Based
Teaching and Learning in a Mid-Size Honors Multivariable Calculus Course
Abstract
At
the 2005 international symposium, Enhancing University Mathematics at
KAIST in Daejeon, Korea, we reported on our ten-year experience of teaching
geometry and calculus courses at all levels using the Internet both for
communication and for demonstrations [B1] At the 2007 ATCM conference in
Taipei, we presented an example of an interactive article on Critical Points
and Curvature based on these courses and this student-developed software [B2].
The purpose of this article is to update those two reports and to present
evidence that interactive Internet-based courses can enhance teaching and
learning at different scales. The primary examples come from a course at Brown
University in the fall semester of 2008 on honors multivariable calculus for a
class of 66 students, twice the number as in previous classes. An extensive
questionnaire at the conclusion of that class provides comparative data that
validate the effectiveness of some earlier modifications and suggest new
directions for pedagogical research.
This report contains four sections:
- 1—Summary of Features of the Tensor for
Internet-Based Teaching and Learning
- 2—The Two-Dimensional Table of Contents and
Improvements in Laboratory Software
- 3—Examples of Student Work Using the Tensor and
Demonstration Software
- 4—Assessment and Future Directions Based on
Comparison of Questionnaire Results
1—Summary
of Features of the Tensor for Internet-Based Teaching and Learning
Several
key features of our approach have been developed primarily in relatively small
classes of approximately 30 students. This past semester, 66 students signed up
for that same course so the scale was different. This necessitated rethinking
several aspects of our courseware, some of which were readily adaptable to a
larger group and several of which open new research questions.
Math
35 has two 80-minute lectures per week, a format more suited to an honors
course where students generally have more background and a longer attention
span than to a standard course where three 50-minute classes per week spreads
out the new ideas in a way that is more easily digestible. For a class of 30
students, it is possible to assign and respond to two assignments per week,
with responses posted online in the Tensor. The first assignment is given out
on the afternoon of the Tuesday class and is to be handed in online by
Wednesday night at 10 p.m. This short assignment gives the students a chance to
see if they have understood the lecture material well enough to solve problems,
as well as to think about the new ideas that are going to be presented on
Thursday. The benefit for the teacher is intermediate feedback that indicates
whether or not it is safe to continue with an idea that most students have
followed up to that point. It also flags certain points of confusion that can
be cleared up at the beginning of the Thursday lecture. After that lecture, a
more substantial problem set is posted, due on Monday morning by 3 a.m. so that
the online responses are ready to be read and commented on by the instructor
(and assistants if available) by Monday afternoon in preparation for the
upcoming week. Up to the time the assignment is due, only the student can view
his or her work and the instructor comments, and after the due time, all
students in the class can read the responses of others, together with comments,
unless some submissions have been designated as “private” (a
feature instituted as a result of requests on questionnaires of previous
courses).
The
Tensor is the piece of communication software where all the responses are
collected. By default only the last five assignments
are presented in a matrix, and selecting "Show All Assignments" will
present all the entries of all students over the course of the semester.
Selecting a week or other heading in the leftmost column with open a matrix for
that assignment, with problems listed on the leftmost column and student user
id initials across the top. Selecting any entry shows the students response and
the comment of the instructor. A square in the matrix is red if the most recent
response came from the student and green if the most recent activity is a
comment from the instructor. Mathematical autobiographies are automatically
private, i.e. so they only available to be read by the instructors of that
class.
One
(unintended) consequence of the ability to respond to comments is that some
students engage in a dialogue until they get all the aspects of a problem
correct. While this is certainly beneficial to the student, it involves extra
time on the part of the instructor. Even without such back-and-forth online
discussion, the practice of providing responses before the beginning of the
next class involves a serious time commitment on the part of the instructor.
Before
class on Tuesday, students are expected to read the comments on their work as
well as the Solution Key, usually a compilation of exemplary (or at least
interesting) responses transferred from student responses by the instructor,
often together with additional commentary. It is possible for students to enter
comments about the work of others in the class, although this aspect is not
often used unless the instructor specifically requests it on certain occasions.
This
commitment on the part of the students and the instructor is substantial and
labor intensive. For 30 students, it is possible to keep up the effort; for 66,
it is far more difficult. There are two major differences that emerged in the
course in the fall of 2008: First of all, students still were faithful and
appreciative about reading comments on their own work, but fewer took the
opportunity to look at the work of other students in the Tensor, relying
instead on the selected responses collected in the Solution Key. Secondly, to a
much greater extent than previously, the course employed group work. Each of
these aspects was treated in the end-of-course questionnaire, and the
assessment based on these data appears in the final section of this paper, where
we also refer to suggestions and comments about the privacy option and the
Solution Key.
One
aspect that did not change was student use of the demonstration software in
assignments and in the interactive laboratories. Under the Resources Menu in
the course webpage, there is a link to the interactive laboratories developed
using the senior thesis of David Eigen, a math-CS concentrator who devised the
program for generating Java applets for use in a variety of mathematics courses
at Brown. The Math 35 page includes a basic tutorial for using the Java demos.
Each section of the labs starts with a labeled picture and a plus sign that can
be selected to see more information about the concept illustrated in the demo
as well as a button that opens a Java applet. The student can explore a
particular phenomenon, entering in new data and manipulating the images. In
order to share what he or she has discovered or created, the student can save
the applet tag and enter it into a homework answer or a discussion. Anyone who
opens the button that appears in the document will enter the program exactly
where the student left off. The instructor or another student can then make
comments, sometimes illustrated by a modification of the given applet.
A
difference from earlier instances this course is the variety of techniques used
by students to enter their responses in the Tensor. As a result of student
suggestions and requests from earlier courses, we included
“shortcuts” to make it easier for students to type mathematical
expression in html. A number of students continued to use this feature
throughout the semester, while others chose to use more sophisticated software,
primarily LaTeX. We also made it more straightforward for students to upload
their written work and many chose to submit their work this way, both in
assignments and in examinations. It is probably worthwhile repeating the
comment made in previous papers that students can immediately type their work
into the Tensor without any significant preparation or instruction, once they
know how to enter exponents and subscripts and a few mathematical symbols for
inequalities and the square root. For example, in the first assignment after
the first lecture, Thunwa Theerakarn
typed in his answer to the following problem:
Problem: What is the range of the function f(x,y) = x2 + 2bxy + y2, defined for all (x,y)? (The answer will depend on b. Try to cover all possible cases.)
Thunwa Theerakarn at 2008-09-07 17:07:43.0
To find the range of the function f(x,y) = x2 + 2bxy + y2, for any y, we can choose t = x + by. Then f(x,y) = t2 + (1- b2) y2
Case |b| ≤ 1 :
Since t2 ≥ 0 and (1- b2) y2 ≥ 0, we have f(x,y) ≥ 0.
Range is all positive real numbers and zero.
Case |b| < 1 :
Since t2 can be any positive real number and (1- b2) y2 can be any negative real number, range of f(x,y) is all real numbers.
Another
feature of the online course that worked well but required extra effort was
giving take-home examinations. There were two mid-term exams, each scheduled
for five days, and a one-week final examination. Such exams routinely include a
number of standard problems, as well as others that are less specifically
defined and more open to interpretation and exploration. It takes a long time
to grade such examinations, since the instructor is responsible for all such
grading. Some examples of more complex problems that can be assigned in such
examinations are given in the next section. In the author’s viewpoint,
these more challenging and open-ended problems can be the most rewarding aspect
of the class, for the students as well as the instructor. They give students a
chance to display a range of thoughtful responses, often leading to multiple
approaches to problems that can be collected in the Solution Key.
Examples
of such open problems and student responses appear in the third section of this
report.
2—The
Two-Dimensional Table of Contents and Improvements in Laboratory Software
A
new feature of our laboratory software is a more explicit two-dimensional table
of contents. Calculus topics appear in the rows of a matrix, with three
columns, for functions of one, two, or three variables. At any point, a student
can navigate from a topic in two-variable calculus “to the left” to
recall the corresponding one-variable topic in a way suitable for
generalization, or “to the right” to see further generalizations
for functions of three and more variables. We continue to look for ways to make
this access tool even more powerful and engaging.
Each
topic listed in the two-dimensional table of contents is in a column according
to its dimension. At any time, a student can move “leftward” from a
laboratory demonstration on two-variable calculus to the corresponding
demonstration for one-variable calculus, or “rightward” to see how
the notion will be extended to functions of three or more variables.
We
illustrate this setup with two examples. The first involves continuity, a
notion that many students understand only imperfectly after a first course in
calculus, especially from a geometric point of view that can be particularly
helpful in calculus of two variables. We interpret continuity as a
challenge-response situation, and in any number of variables, the process is
the same. Given a function f(x) of one variable and a point x0 of
the domain, the challenger chooses a pair of horizontal lines at distance
ε from y = f(x0) and asks if the domain can be restricted to
points with distance less than δ from x0 so that the graph over
that restricted domain lies between the two horizontal lines. If every
challenge can be met, then the function is continuous at x0. In the
case of a function of two variables, the challenge is the same, except that
there are two horizontal planes at distance ε from the plane z = f(x0,y0) and the responder has to choose
δ so small that the graph over the disc of radius δ centered at (x0,y0)
lies between the planes.
Another
example refers to the author’s paper in Volume 2, Number 2 of eJMT. Critical points of a function of one variable can be
visualized by coloring the graph of a function f(x) red if the derivative
f’(x) is positive. Similarly critical points of a function of two
variables can be visualized by coloring the graph of a function f(x,y) red if fx(x,y) is positive, blue if fy(x.y) is positive, and purple if both are positive.
An
example appears in the interactive article [B1] concerning the topic of
critical points. Students are familiar with Rolle’s theorem for a
function f(x) of a single variable, stating that such a continuous function
defined over an interval a ≤ b must have an interior local maximum or
minimum or both if f(a) = f(b). To generalize this, consider a continuous
function f(x,y) defined on a
region D bounded by a curve C on which the function f is constant. The
conclusion is that there must be a local maximum or a local minimum or both in
the interior of D. If the function of one variable is differentiable, then the
derivative of f must be zero at any interior local
maximum or minimum so the tangent line is horizontal there. For a function of
two variables, all partial derivatives at in interior local maximum or minimum
must be zero and the tangent planes at such points must be horizontal. Students
can then be challenged to state and prove generalizations of the Mean Value
Theorem, where a differentiable function f(x,y) coincides with a linear function L(x,y) = ax + by + c on the boundary C curve of a disc domain
D. More complex questions deal with the number of critical points of various
types for functions that are assumed to be non-negative on a domain and zero on
the boundary. In the case of one variable, if the critical points are isolated
maxima and minima, then the number of maxima is one greater than the number of
minima. For the corresponding two-dimensional theorem, if all critical points
are m0 local minima, m1 ordinary saddles, and m2
local maxima, then students can explore and come up with the conjecture that m2
– m1 + m0 = 1, a powerful and important result
popularized by Marston Morse and reported in [M].
Interactive
Laboratories: Under the Resources Menu in the course webpage, there is a link
to the interactive laboratories developed using the senior thesis of David
Eigen, a math-CS concentrator who devised the program for generating Java
applets for use in a variety of mathematics courses at Brown. The Math 35 page
includes a basic tutorial for using the Java demos. Each section of the labs
starts with a labeled picture and a plus sign that can be selected to see more
information about the concept illustrated in the demo as well as a button that
opens a Java applet. The student can explore a particular phenomenon, entering
in new data and manipulating the images. In order to share what he or she has
discovered or created, the student can save the applet tag and enter it into a
homework answer or a discussion. Anyone who opens the button that appears in
the document will enter the program exactly where the student left off. The
instructor or another student can then make comments, sometimes illustrated by
a modification of the given applet.
3—Examples
of Student Work Using the Tensor and Demonstration Software
Examples
of such investigations from the Tensor appear in the work of Soravit Changpinyo and Thunwa Theerakarn, both students
from Thailand in my honors multivariable class.
Problem: Analyze the function f(x,y) = xy(1
- x2 - y2) showing the graph of the function together
with its zero contour, and identify the critical points of the function. What
is the maximum value taken on by the function on the domain consisting of all (x,y) with x2 + y2
≤ 4?
Soravit Changpinyo solves part (a) really
well:
f(x,y) = xy(1-x2-y2)
f(x,y) = 0 when x=0 or y =0 or x2 + y2 = 1
Its zero contour is along the light blue curve, two linear lines and a circle.
fx(x,y) = xy(-2x) + (1-x2-y2)y
= -3yx2 + y – y3
fy(x,y) = xy(-2y) + (1-x2-y2)x = -3xy2
+ x – x3
fx(x,y) = -3yx2
+ y – y3 = 0
y(1-3x2-y2) = 0
(1) y = 0 or
(2) 3x2+y2 = 1
fy(x,y) = -3xy2 + x – x3 = 0
x(1-3y2-x2) = 0
(3) x = 0 or
(4) 3y2+x2 = 1
The critical points are all (x,y) such that fx(x,y) = 0 and fy(x,y) = 0
They could be represented by the intersections of two ellipses (3x2
+ y2 = 1 and 3y2 + x2 = 1), the intersections
of two lines (the x-axis and the y-axis), and the intersections of the line and
the ellipse of different colors.
Solve for (x,y)
from (1) and (3); (0,0)
Solve for (x,y) from (1) and (4); (-1,0), (1,0)
Solve for (x,y) from (2) and (3); (0,1), (0,-1)
Solve for (x,y) from (2) and (4); (0.5,0.5),
(-0.5,0.5), (0.5,-0.5), (-0.5,-0.5)
The critical points are (0,0,0), (-1,0,0), (1,0,0), (0,1,0), (0,-1,0), (0.5,0.5,0), (-0.5,0.5,0), (0.5,-0.5,0), (-0.5,-0.5,0).
0 <= x2 + y2 <= 4
-3 <= 1 - x2 - y2 <= 1
(|x|-|y|)2 = x2 - 2|xy| + y2
>= 0
2|xy| >= 4
|xy| <= 2
-2 <= xy <= 2
xy and 1 - x2 - y2
must have the same sign so their product is positive.
if both xy and 1 - x2 - y2 are
positive, the possible maximum of the product is (1)(2) = 2.
if both xy and 1 - x2 - y2 are
negative, the possible maximum of the product is (-2)(-3)
= 6.
The maximum value taken on by the function on the domain consisting of all (x,y) with x2 + y2 <= 4 is 6.
The demo below shows that there are two maximum points. Both of them satisfy x2 + y2 = 4.
[applet]
Problem: What can you say about the function g(x,y) = x4 – 6x2y2 + y4 . (Standard Hint: look at the graph.)
Thunwa Theerakarn used standard Macintosh graphing hardware to produce images that he included in his assignments :

Graph of g(x,y) = g(x,y) = x4 – 6x2y2 +
y4
With plane cut through g(x,y) = 0. The view is from above looking down to xy-plane.
We will see that the plane divides the surface into 8 symmetrical pieces, 4
above and 4 below.

Make a conjecture that g(x,y) can be written in cos(4θ) form in polar coordinates.
Consider
g(x,y) = x4
– 6x2y2 + y4 .
= r4cos4θ - 6r4cos2 θsin2θ
+ r4sin4θ
= [r4cos4θ - 2r4cos2θsin2θ
+ r4sin4θ] - 4r4cos2 θsin2θ
= [r4[cos2θ -sin2θ]2] - r4sin2
(2θ)
= r4[cos2 (2θ)2 - r4sin2
(2θ)
= r4cos(4θ)
Therefore, zero contour level is lines cos(4θ) = 0, that is, the lines θ = π/8 , 3π/8 , 5π/8 , 7π/8, 9π/8, 11π/8, 13π/8, 15π/8.
It
might be interesting to some readers to look at the responses of these two
students to the initial questionnaire for the course: In Soravit’s
Mathematical Autobiography, written the first day of the course, he states:
“There are three things I expect from this class. The first thing is
challenging stuff. Math that’s too easy isn’t fun. Another thing is
a strong foundation in calculus that will ease my learning in computer science.
Lastly, I would like to learn about math not only from the instructors, but
also from my peers. I know everyone is exceptionally talented.” He
indicated in his questionnaire that my course had been recommended to him by
Saran Ahuja, a member of the Thai Mathematical Olympiad team when he was a
student at the Montford School in Chiangmai, and one of the top students in my
course in Honors Linear Algebra during his first semester at Brown three years
ago.
Thunwa writes “At the end of my high school years, I won a
Thai Government scholarship to study in the United States from undergrad to
Ph.D. The scholarship requires me to earn degree on Applied Mathematics and I
will have to work in a university in Thailand for twice as time I will have
spent here. This course will be hard - I know. Somebody told me I should not
start first year in college with a hard course. But... there's so much to
learn, and I'm willing to learn it. As always, it will be challenging, fun, and
beautiful.
Problem: Find the points of the ellipse x2 + xy + y2 = 1 closest to the origin and furthest from the origin by finding the critical points of f(x,y) = x2 + y2 on the ellipse. (See the Hint to recall the procedure for Lagrange multipliers.)
Solution to Problem:
Let g(x,y) = x2 + xy + y2
f(x,y) = x2 + y2
Consider the minimum and maximum of f(x,y) on level curve g(x,y) = 1
Using Lagrange multipliers,
∇f(x,y) = λ ∇g(x,y)
∇f(x,y) = (2x,2y)
∇g(x,y) = (2x+y,2y+x)
2x = λ(2x+y) and 2y = λ(2y+x)
That is 2x/(2x + y) = 2y/(2y + x)
that is x2 = y2
Case x = y
from g(x,y) we get that x2 + x(x) + x2
= 1
That is 3x2 = 1
x = 1/√3
(x,y) = (1/√3,1/√3) , (-1/√3,-1/√3)
f(x,y) = x2 + y2 = 2/3
Case x = -y
From g(x,y) = 1, we get that x2 = 1
That is x = ±1
(x,y) = (1,-1) , (-1,1)
f(x,y) = x2 + y2 = 2
Therefore, g(x,y) closest to the origin at (x,y) = (1/√3,1/√3) , (-1/√3,-1/√3)
and furthest at
(x,y) = (1,-1), (-1,1).
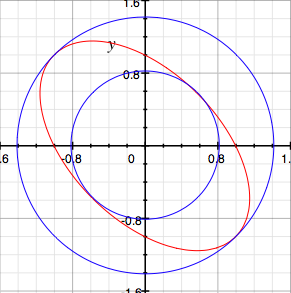
Problem: Find the critical points of the function f(x,y,z) = x2 + y2
+ z2 on the ellipsoid x2 + y2/4+ z2/9
= 1 and indicate whether they are maxima or minima or other.
Here is a demo intended to give some inspiration. Changing r will alter the
radius of an expanding sphere, representing the contour surfaces of f(x,y,z). What happens when the
sphere and the ellipsoid intersect?
[applet]
Solution to Problem:
f(x,y,z) = x2 + y2 + z2
Let g(x,y,z) = x2 + y2/4 + x2/9
Consider the critical points of f(x,y,z) on the level set of g(x,y,z) = 1
Using Lagrange multipliers
∇f(x,y,z) = λ∇g(x,y,z)
That is (2x+2y+2z) = λ(2x+y/2+2z/9)
implies
2x = λ2x
2y = λy/2
2z = λ2z/9
That is
x = 0 or λ = 1
y = 0 or λ = 4
z = 0 or λ = 9
Consider that in each case, λ cannot be the same constant. Therefore, two of {x,y,z} have to equal zero in each case.
When x=0, z=0, y=±2
f(x,y,z) = 4
When x=0,y=0 , z=±3
f(x,y,z) = 9
When y=0, z=0 , x=±1
f(x,y,z) = 1
Therefore, (0,0,±3) are maxima, (±1,0,0) are minima and (0,±2,0) are critical points but not maxima or minima.
At the critical points, the gradient vectors of f and g are parallel
Critical Points at Level f(x,y,z)
= 2
We
take our final illustration from one of the problems on the midterm
examination. The first examination in the course took place four weeks after
the start of the semester. The Midterm Examination was a take-home test over a
period of six days. It consisted of ten problems, each with two or three parts,
and students were permitted to use notes and books and computers, as well as
all the material on the class website, but they all agreed that no one would
consult anyone else, either in person or electronically.
The
first problem required students to identify the critical points of a polynomial
function f(x,y) = x4
– 2x2 – y2 and to find the maximum and
minimum values on a disc of radius R centered at the origin, where the result
depended on R.
The
last part of the problem was subtle enough to test the ingenuity of most
students. William Fallon devised a demonstration that was particularly useful
in seeing how the image of a disk of radius R changed with R,
[applet]
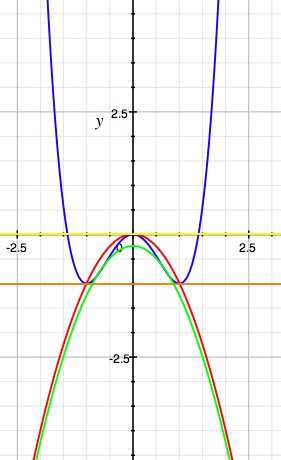
Gili
Kriger was able to construct a two-dimensional graphic showing five different
functions of R on the same diagram, from which it was possible to read off the
required maxima and minima, and to provide algebraic justification for the
listing of results.
4—Assessment
and Future Directions Based on Comparison of Questionnaire Results
Recent
proposals to the Division of Undergraduate Education of the National Science
Foundation have placed special emphasis on developing effective assessments of
the teaching and learning aspects of the project, particularly in the
dissemination phase. Potential users of the technology need to know the results
of our experience, and the ways in which we have modified the course, the
technology, and the assessment instruments, so that they can determine whether
and how this approach might be adapted to their needs and the needs of their
students and institutions.
Course
evaluation data have been collected in more than twenty courses using this
approach, mostly at Brown University but also at Yale University, the
University of Notre Dame, UCLA, and at the University of Georgia, both in the Mathematics department and in the College of Education. In
2004, we redesigned our questionnaires with the help of a professional market
researcher who specializes in analysis of qualitative data. She has developed a
method for systematically analyzing the data using a form of content analysis
which enables us to summarize and display our results, course by course as well
as for the same course across semesters and teaching situations (i.e.,
different teachers, different schools). These data collection techniques and
methods of analyses represent a substantial improvement over our earlier
assessment efforts.
For
each course, the data were aggregated into question-by-question spreadsheets;
responses for each question part, or sub-question, were coded (positive,
neutral, and negative using a three-point scale) and displayed next to the
individual verbatim response. Finally, summary tables were generated for each
question by sub-questions. In this method of analysis, some comments within
verbatim responses could be highlighted for making summary points in the data
tables, and for use in reports and presentations.
(Verbatim
comments were only reported for students who had handed in a written statement
giving the instructor permission to use submitted work in presentations and
reports.)
Examining
coded verbatim responses for each question reveals patterns in students’
responses within a course. Summary tables of codes by question and sub-question
yields the more substantive analysis, and results for the same question or
sub-parts of a question can be compared across time. Examining the data in
these several systematic ways establishes a basis for deciding how to adapt and
improve the teaching technology and interactive process for students and the
teaching situation for the instructor.
Response
rates for the two courses were comparable; in Fall 2004, 39 of 60
students completed course evaluations (65%), and in Fall 2008, course
evaluations were received from 54 of 63 students who completed the course (86%).
In
2004, the questionnaire included nine questions (with up to four sub-parts),
covering: 1) online assignments, 2) solution keys and hints 3) online student
interaction 4) online communication with instructors 5) timing of assignments
6) examinations 7) textbook 8) visualization software (“demos”),
and 9) an additional open-ended question allowing for general comments. In
2008, question 7 was altered since there was no specific text for the course,
and a tenth question was added concerning the policy of working in groups for
the bi-weekly homework assignments (a new procedure introduced in 2008).
In
2004, students submitted their course evaluations online after they completed
classes and before completing their final exam, while in 2008, students
submitted their course evaluations online just after completing a final
take-home exam, with the understanding that the questionnaires would only be
read after the grades had been determined.
Analysis of the Question on Comfort Level
for Sharing Work Online
The
value of this assessment method can be illustrated with an analysis of
responses to an important question we asked about our teaching and learning
approach, namely how “comfortable” students are with opening their
work to other students online. This element of viewing the work of their
classmates, and instructor comments is central to our model of teaching and
learning. We also asked if students if their attitudes had changed over time.
In
the 2004 questionnaire, some students expressed discomfort at having their work
on assignments and examinations, as well as instructor comments (but not
grades) available for others to read. In subsequent courses, the software was
modified so that students are given the option to designate any particular
response “private”, so only readable by instructors. Responses to
the analysis of other questions have also led to modifications and refinements;
we expect this to continue during the dissemination phase of our project.
Table 1. Learning from other
Students
Honors
Multivariable Calculus
|
a.
How often did you look at the work of other students? |
Fall |
|
Fall |
|
(Base: #
Respondents) |
(39) |
|
(54) |
|
“Usually” |
14 |
|
7 |
|
b. Did you look at the work of some students more often
than others? If so, how did you decide whose work to look at? |
|||
|
(Base: #
Respondents) |
(39) |
|
(54) |
|
“No” |
8 |
|
12 |
|
c. How comfortable were you with having your homework
available for other students to read? |
|||
|
(Base: #
Respondents) |
(39) |
|
(54) |
|
“Okay”/“no
problem” |
34 |
|
36 |
|
d.
How comfortable were you with having your exams available for other students
to read? |
|||
|
(Base: # Respondents) |
(39) |
|
(54) |
|
“Okay”/“no problem” |
30 |
|
28 |
Several students reported changes in their attitudes over time. Most interesting is the student who said:
"In the beginning I
really did not like the system of reading other student homework. It made
me feel really nervous and exposed and it made me want to leave problems blank
rather than to put in an incorrect answer. As the semester progressed
I realized what a useful tool it could be and I started reading other people's hw responses more and more and felt more comfortable with
mine being read."
Another
student addressed motivation:
"It didn't really bother
me that other people could look at my work, either at the beginning or the end
of the semester. Sometimes I felt bad about the quality of the work that
I handed in and I might have preferred that others not look at it, but it
didn't concern me enough to make me want to change the system and the
motivation to do a better job probably didn't hurt either."
As
the numbers indicate, some students felt differently about exams:
"I think I am more
self-conscious about my exams. At first I didn't mind
so much, but now I am beginning to think that there should be some element of
privacy with exams, or a way to choose to have your exam available or
not".
A
counter-intuitive response was:
"I have always been
self-conscious about having work of mine open to criticism, so I was slightly
uncomfortable (about the homework being available)" but "On exams, I was able to put
more time into refining my answer, so I didn't mind having people see
that."
Analysis of the Questions on Group Work for Assignments
A
major change in the communication aspect of the course is the requirement that
students participate in homework groups for their bi-weekly assignments,
resulting in a manageable 20 or so responses instead of 66. Comfort
levels on making homework responses public rose slightly, although most
students reported sharing primarily within the group rather than reading other
entries in the Tensor. A number of students appreciated selecting certain
student answers for the Solution Key for each assignment. There was still some
dissatisfaction with making examination answers available for everyone in the
class to read. On the basis of this information, we will alter the software so
that it will be possible for a student to designate the totality of his or her
examination responses as private, rather than having to make this designation
on each separate question.
Table 2. Sample Groups A and
H
|
Briefly,
describe the way that you worked [in your homework group]: |
|||||||
|
|
|
|
10.a |
10.b |
10.c |
||
|
Group |
ID |
|
a) Who was in your homework group?
How often did you meet in person? How many attended in-person sessions? How
did your meetings change over the semester? |
b) What problems, if any,
did you experience with the group process? Any suggestions for improving it? |
c) How comfortable were you
working in the group? Did your feelings change? |
||
|
A |
amc
|
2 |
kmd,
a person in my dorm. We met about twice a week, always in person. |
OK
|
None really. |
OK
|
It was very helpful for me at
time. We sometimes thought up some clever stuff together. |
|
A |
kmd
|
2 |
I was in a group with amc. ... we would meet the night it was due and clear up
any problems that we had. Usually ... about a half
hour or so (occasionally much longer if we had lots of questions). As the
course progressed I found that I typically was the
one who was typing up the problems which was fine because that was how I like
to do the problems anyway. |
+/-
|
I felt as though groups can
benefit certain people more than others. Typically
one person will have more problems with the homework than others which means
that one person will spend most of the time explaining to other people which
is less beneficial for them. |
OK
|
I felt very comfortable working in
the group. |
|
H |
mlw
|
5 |
For the majority of the assignments I worked with [names] ... since I ... worked a
lot with [names] in physics class and we worked well together. We usually met
pretty consistently every Sunday and Wednesday in person to do the homework. |
OK
|
The group worked great for me. |
OK
|
In the beginning I was not excited
about having to do the homework in groups, but it turned out to be very
useful. Especially when the problems were conceptually difficult it was
really beneficial having lots of people thinking about it and eventually talking
it out rather than potentially getting stuck not starting a lot more
problems. Having to explain our thinking seemed to make everyone grasp the
material better since its a lot easier to write
faulty logic than talk other people through it. |
|
H |
adp
|
5 |
Me, [names] ... We met once for
each assignment we were allowed to do in groups, but not otherwise. Everyone
showed up, and we'd split up the problems but everyone would check everyone
else's work |
OK
|
None except that it made the
non-group process seem more difficult |
OK
|
consistently comfortable |
|
H |
bal
|
5 |
[names] ... were in my group. We
met in person for almost every homework assignment towards the end of the
semester. Not that frequently at the beginning. We all attended the sessions.Our meetings became
more productive over the semester. |
OK
|
The geographic organization of
groups is a good starting point. It's much easier to work with people who you
live near. |
OK
|
I was more comfortable towards the
end of the semester. The first group meeting was awkward and we didn't work
as well since we were just getting to know one another. |
|
H |
rpp
|
5 |
My core homework group consisted
of [names] ... and myself. We met twice a week and usually worked out any
problems we were having with the homework, then split the writing up of the
problems between us. The homework group was a great asset to me; the other
people in my group usually provided a fresh perspective on a problem that had
become stagnant in my mind. The spreadsheet that listed students by their
physical location was instrumental in arranging the groups; I would
definitely make it a point to create one of these for all future classes. |
OK
|
I had no problems whatsoever and
very much enjoyed working with my group. |
–
|
[no answer] |
|
H |
jwb
|
5 |
I rarely participated in my group
as the rest of [residence hall] seemed to have a very different schedule from
me. |
–
|
[no answer] |
+/-
|
I liked it when I participated,
but it wasn't really practical for me. |
Table 3. Sample Summary
Results on Group Work (Q10C)
|
How comfortable were you working in the group? Did
your feelings change? |
|
|
78%
were comfortable working in the group |
|
|
● |
17 out of 54 --
33% -- found their group's process "comfortable" and cited specific
advantages. |
|
● |
15 out of 54 --
28% -- said "comfortable" / "fine" / "no
problem" /"liked it". One noted that group work "didn't
help much with the math." |
|
● |
10 out of 54
respondents -- 19% -- got MORE comfortable with their group's process as the
semester went on. |
|
13%
made negative comments about working in groups |
|
|
● |
Most (4 out of 7)
commented about "inefficiency". |
|
● |
Only one person
complained that group work meant "being asked to give others credit for
my work". |
|
5
out of 54 -- 9% -- did not participate in a group, or did not answer the
question. |
|
Responses
to the question about group work suggest a number of modifications in the
Tensor software that can facilitate further interaction. The author
intends to work in the next stage of this project with colleagues Barbara
Reynolds of Stritch University [R], an expert on group processes in mathematics
instruction, and Thomas Cooper, who has designed and studied modifications of
the Tensor software for enabling group interaction in pre-calculus courses in a
non-residential college [C].
Many
thanks to Michael Schwarz for his help in preparing this article.
References
|
[B1] |
Banchoff,
Thomas, “Interactive Geometry and Multivariable Calculus on the
Internet”, Proceedings of the KAIST International Symposium on
Enhancing Undergraduate Teaching of Mathematics, Daejon, Korea, (2005),
11-31. Reprinted in Enhancing University Mathematics: Proceedings of the
First KAIST International Symposium on Teaching, AMS series CBMS Issues in
Mathematics Education, CBMATH-14, (2007), 17-32. |
||
|
[B2] |
Banchoff,
Thomas, “Interactive Geometry and Critical Points” The Electronic
Journal of Mathematics and Technology, Volume 2, Number 2 (2008). |
||
|
[C] |
Cooper, Thomas E., “Student
Interactions during Asynchronous Problem Solving Using a Communication
Tensor” (2008) Ph. D. Thesis, University of Georgia. |
||
|
[R] |
Dubinsky, Ed, Ed.; Mathews, David,
Ed.; Reynolds, Barbara E., Ed. Readings in “Cooperative Learning for
Undergraduate Mathematics”, MAA Notes No. 44 (1997). |